Shinhoo Kang

Shinhoo Kang

Assistant Professor of Computer Convergence Software at Korea University Sejong Campus

Research

My research primarily focuses on conventional scientific computing and how it can be applied to multiphysics and multiscale problems such as computational fluid dynamics and Earth system modeling. My interests include entropy stable methods, operator splitting methods, high-order methods, and high-performance computing. Nowadays I turn my attention to scientific machine learning (SciML) because of its significant impact on science and engineering. Combining traditional scientific computing and machine learning methods, SciML leverages the strengths of both fields and bridges the gap between them, providing new and innovative perspectives for solving complex problems in a variety of scientific and engineering applications. I think SciML can be a good complementary of traditional numerical models. Accordingly, I am actively working on developing surrogate models for geophysical flows.

Research Highlights

Learning SGS Models in DG with NODE

The growing computing power over the years has enabled simulations to become more complex and accurate. However, high-fidelity simulations, while immensely valuable for scientific discovery and problem solving, come with significant computational demands. As a result, it is common to run a low-fidelity model with a subgrid-scale model to reduce the computational cost, but selecting the appropriate subgrid-scale models and tuning them are challenging. We propose a novel method for learning the subgrid-scale model effects when simulating partial differential equations using neural ordinary differential equations in the context of discontinuous Galerkin (DG) spatial discretization. Our approach learns the missing scales of the low-order DG solver at a continuous level and hence improves the accuracy of the low-order DG approximations as well as accelerates the filtered high-order DG simulations with a certain degree of precision. We demonstrate the performance of our approach through multidimensional Taylor–Green vortex examples at different Reynolds numbers and times, which cover laminar, transitional, and turbulent regimes. The proposed method not only reconstructs the subgrid-scale from the low-order (1st-order) approximation but also speeds up the filtered high-order DG (6th-order) simulation by two orders of magnitude.

We developed a differentiable DG solver on a structured mesh for compressible Navier–Stokes equations. Taylor-Green vortex example is shown in Figure at $Re=1600$.

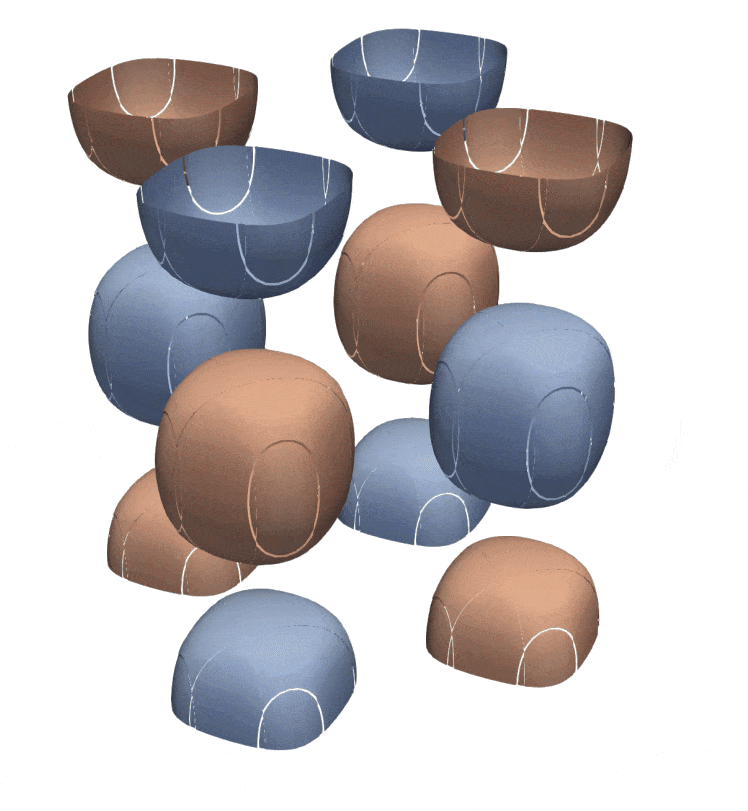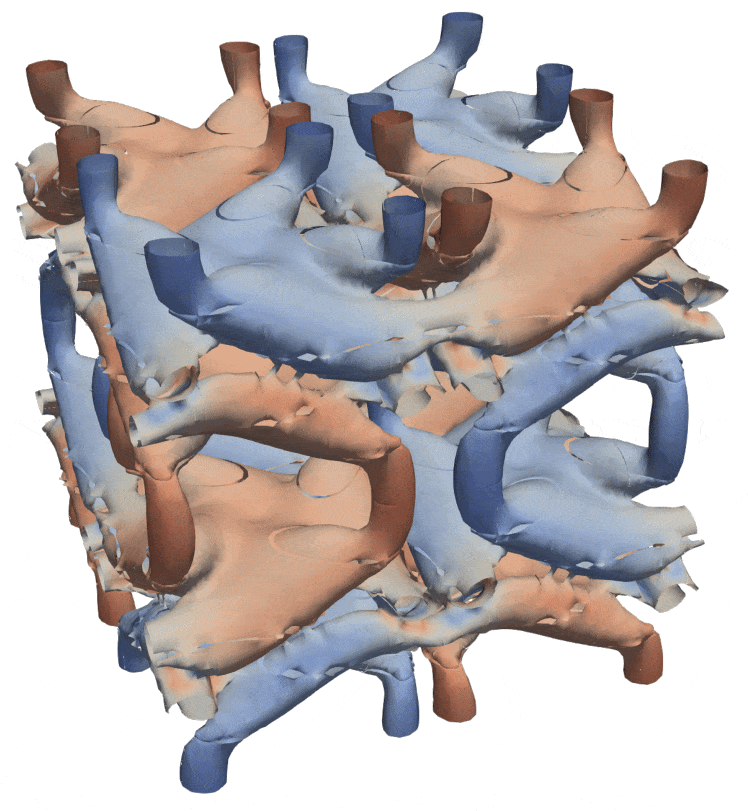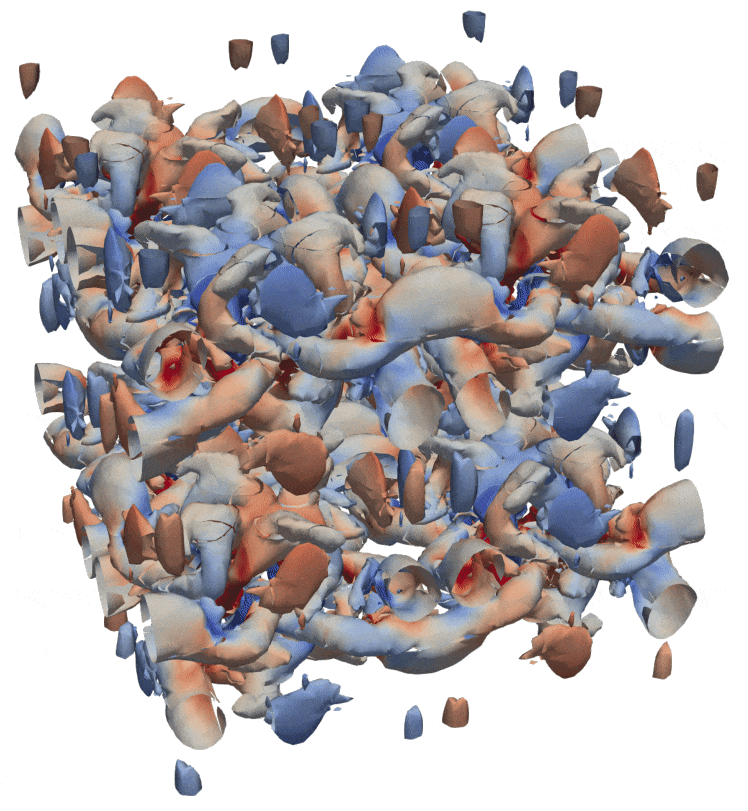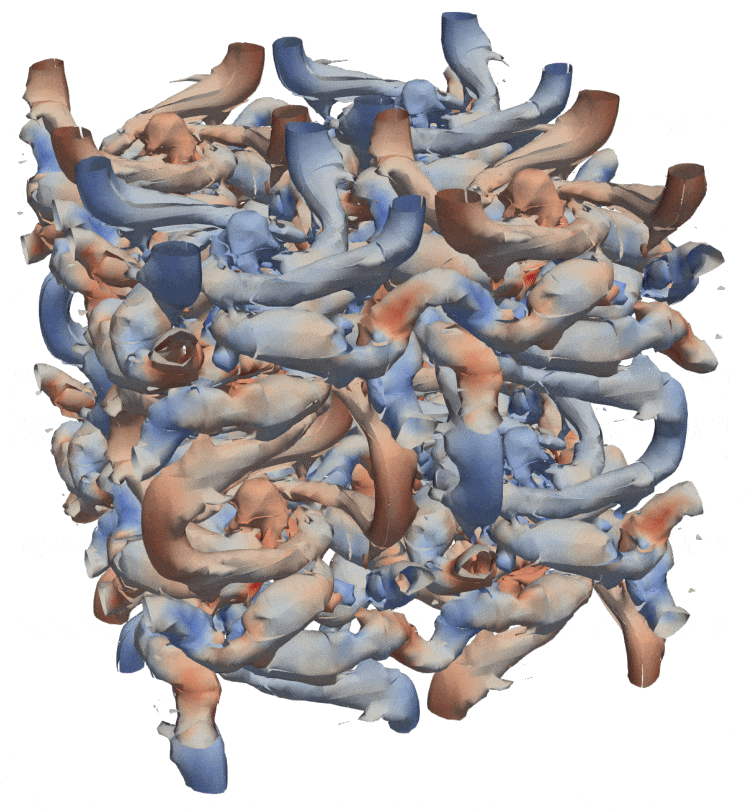
We see the remarkable improvements in the snapshots at $t=8$. The augmented solution successfully recovers the vortical structures, whereas the low-order solution quickly loses the vortices due to the numerical dissipation associated with the low-order solver in the viscous-dominated flows ($Re=100$).

Learning Subgrid-scale Models with Neural Ordinary Differential Equations

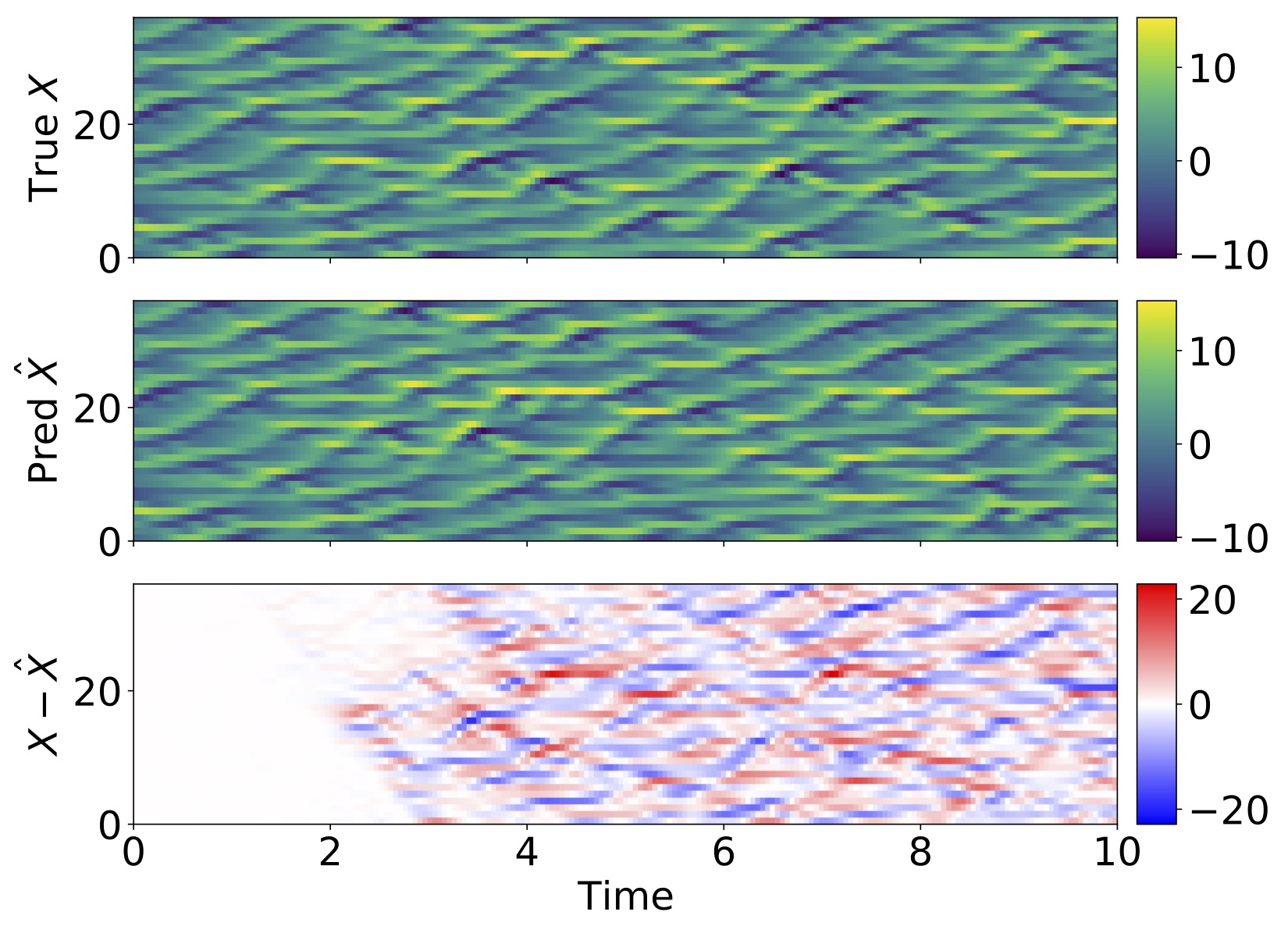
We propose a new approach to learning the subgrid-scale model when simulating partial differential equations (PDEs) solved by the method of lines and their representation in chaotic ordinary differential equations, based on neural ordinary differential equations (NODEs). Solving systems with fine temporal and spatial grid scales is an ongoing computational challenge, and closure models are generally difficult to tune. Machine learning approaches have increased the accuracy and efficiency of computational fluid dynamics solvers. In this approach neural networks are used to learn the coarse- to fine-grid map, which can be viewed as subgrid-scale parameterization. We propose a strategy that uses the NODE and partial knowledge to learn the source dynamics at a continuous level. Our method inherits the advantages of NODEs and can be used to parameterize subgrid scales, approximate coupling operators, and improve the efficiency of low-order solvers. Numerical results with the two-scale Lorenz 96 ODE, the convection–diffusion PDE, and the viscous Burgers’ PDE are used to illustrate this approach.

Hovmöller diagram of the true model (top) and the trained model (middle) for the slow variables of two-scale Lorenz 96 system. The bottom panel shows the difference between the two simulations.

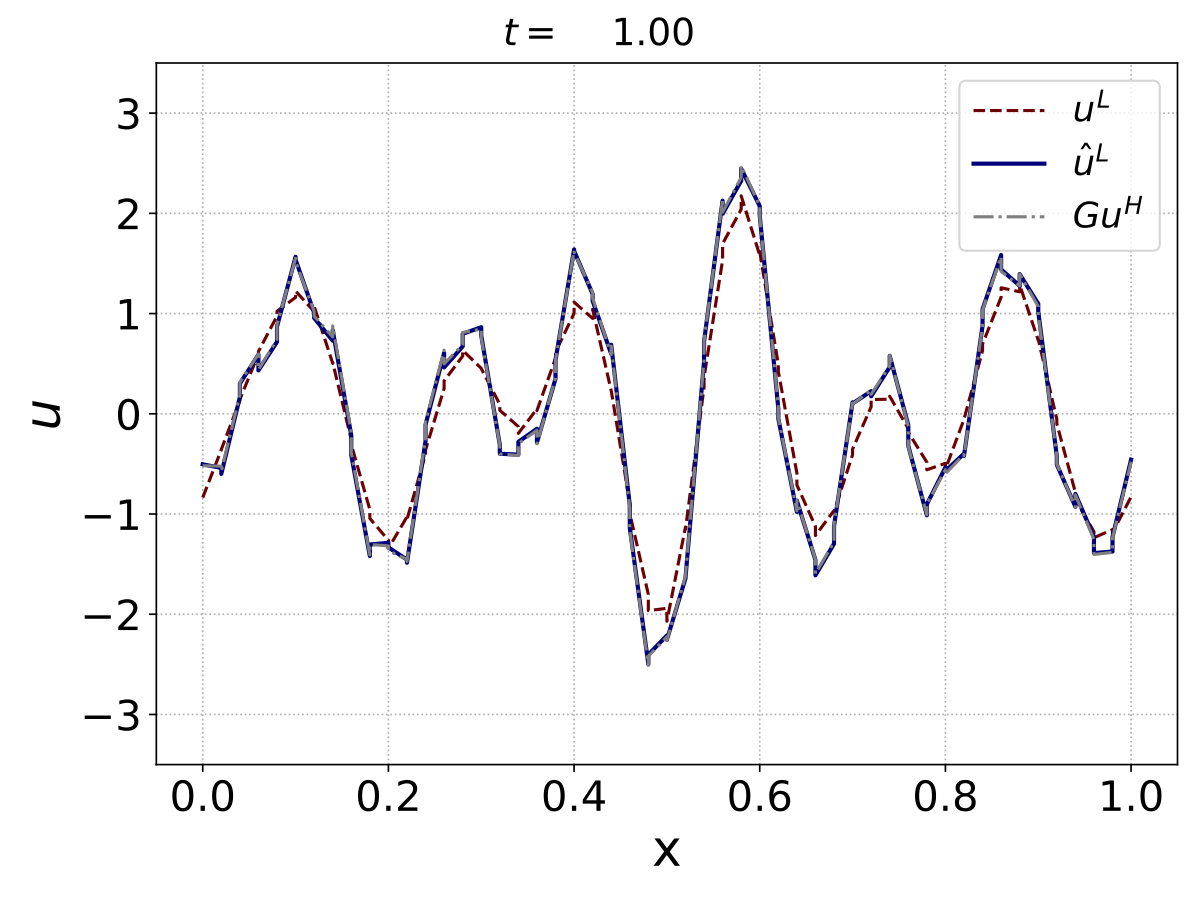
We show the snapshot of $u^L$, $\hat{u}^L$, and $Gu^H$ at the final time ($t=1$). We note that the neural network source term helps maintain a less smooth (polygonal) waveform of the filtered solution, when compared with the first-order DG method without the source term.

The following figure shows the relative errors of $\hat{u}^L$ (red dot line) and $\tilde{u}^L$ (blue dash dot line) against timestep sizes. In general the continuous corrective forcing approach demonstrates better accuracy than the discrete corrective forcing approach. The error of $\hat{u}^L$ converges to a certain nonzero constant with decreasing $\triangle t^L$. The error of $\tilde{u}^L$, however, does not show any convergence; rather, it has the minimum relative error at $\triangle t^L=10^{-3}$ in which discrete corrective forcing was trained.

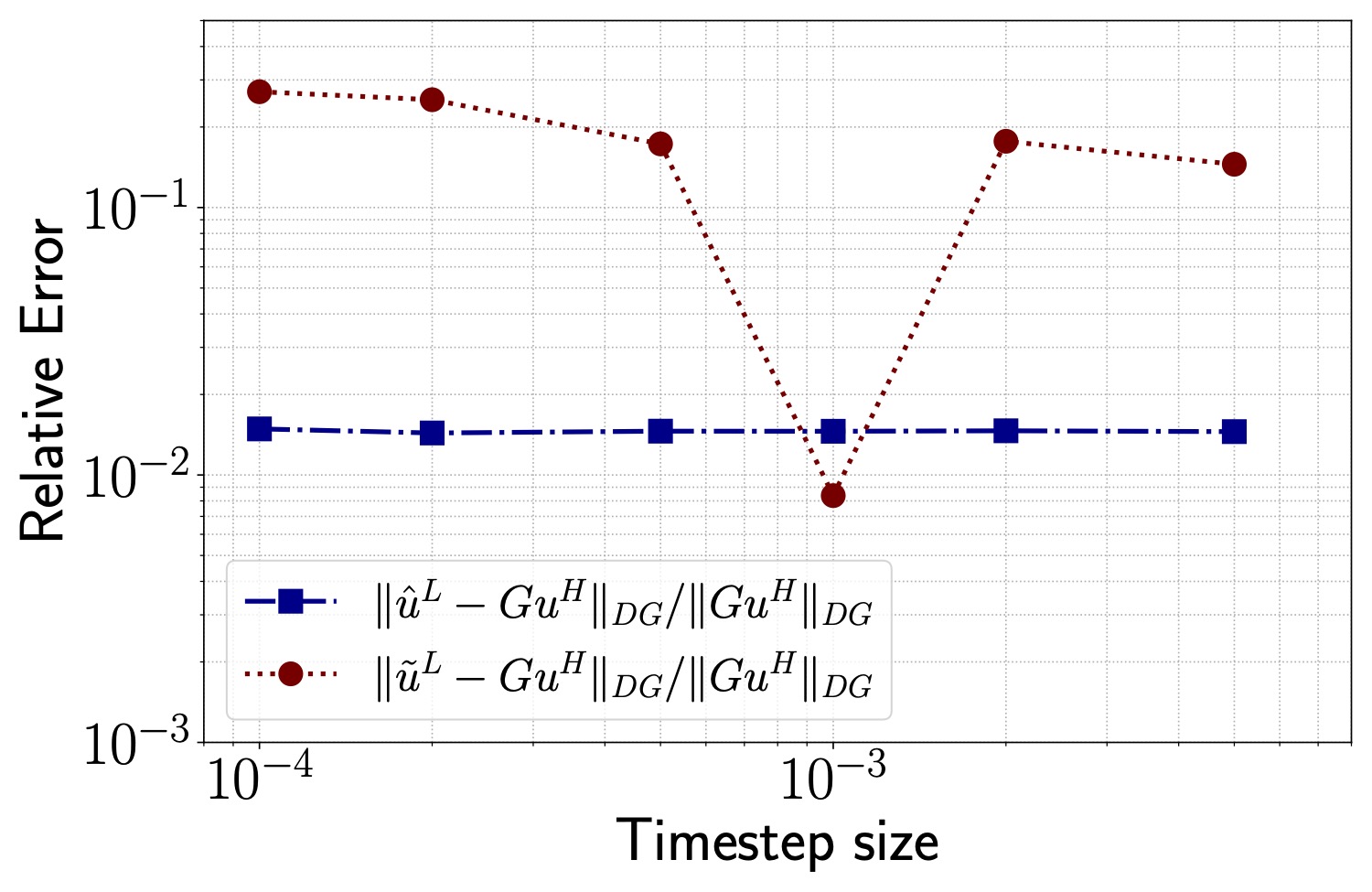
This is expected because the discrete corrective forcing approach learns a map from the low-order solution to the corrective forcing approximation with a specific timestep size and the first-order Euler method. Thus, predicting with different $\triangle t_L$ degrades performance. On the other hand, the neural ODE approach learns the corrective forcing operator at a continuous level. This leads to consistent results that do not degrade the simulation predictability by changing the timestep size

Multirate Coupling Methods

we propose to apply multirate partitioned Runge-Kutta (MPRK) coupling methods for fluid-fluid interaction problems. We propose using multirate partitioned Runge-Kutta (MPRK) coupling methods for fluid-fluid interaction problems. A buffer region is employed at the interface to ensure a smooth transition, which is essential for conservation and convergence. Our solution adds only a little amount of complexity to a singlerate implementation while providing the complete computational benefit of a multirate method. We develop a theoretical performance model for both serial and parallel instances to measure computing performance systematically. The usefulness of using multirate methods for solving coupled compressible Navier-Stokes equations (CNS) has been demonstrated through several numerical studies.

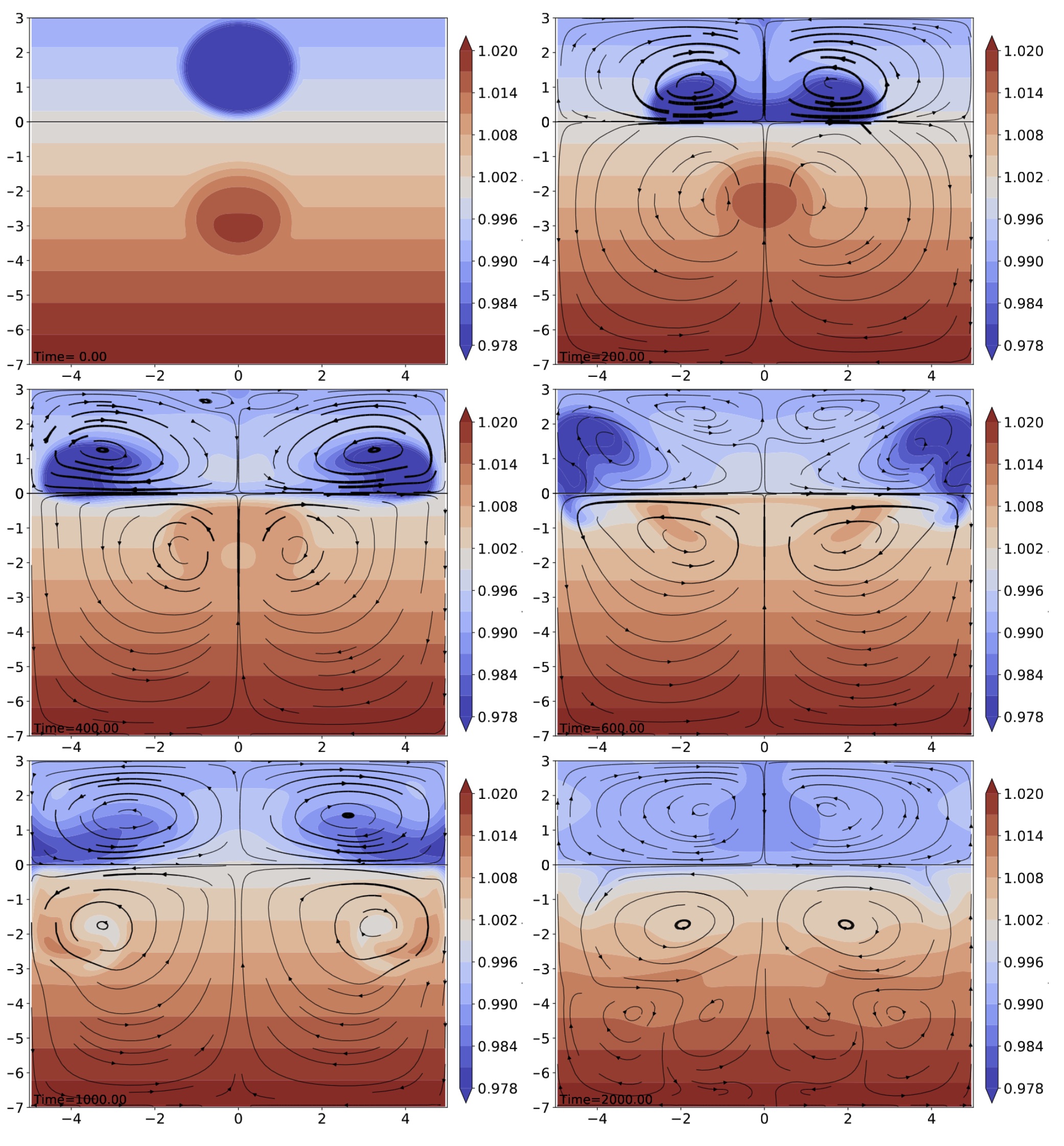
We perform the simulation with the MPRK2 ($m=4$) method. The evolution of temperature fields is shown for $t\in{0,2000}$. The cold fluid parcel in the atmosphere drops down to the interface while the warm fluid in the ocean rises. The cold and warm perturbations horizontally move balancing heat and momentum fluxes across the interface, and hit the walls. The cooled fluid on the ocean surface begins to sink and create circulations.

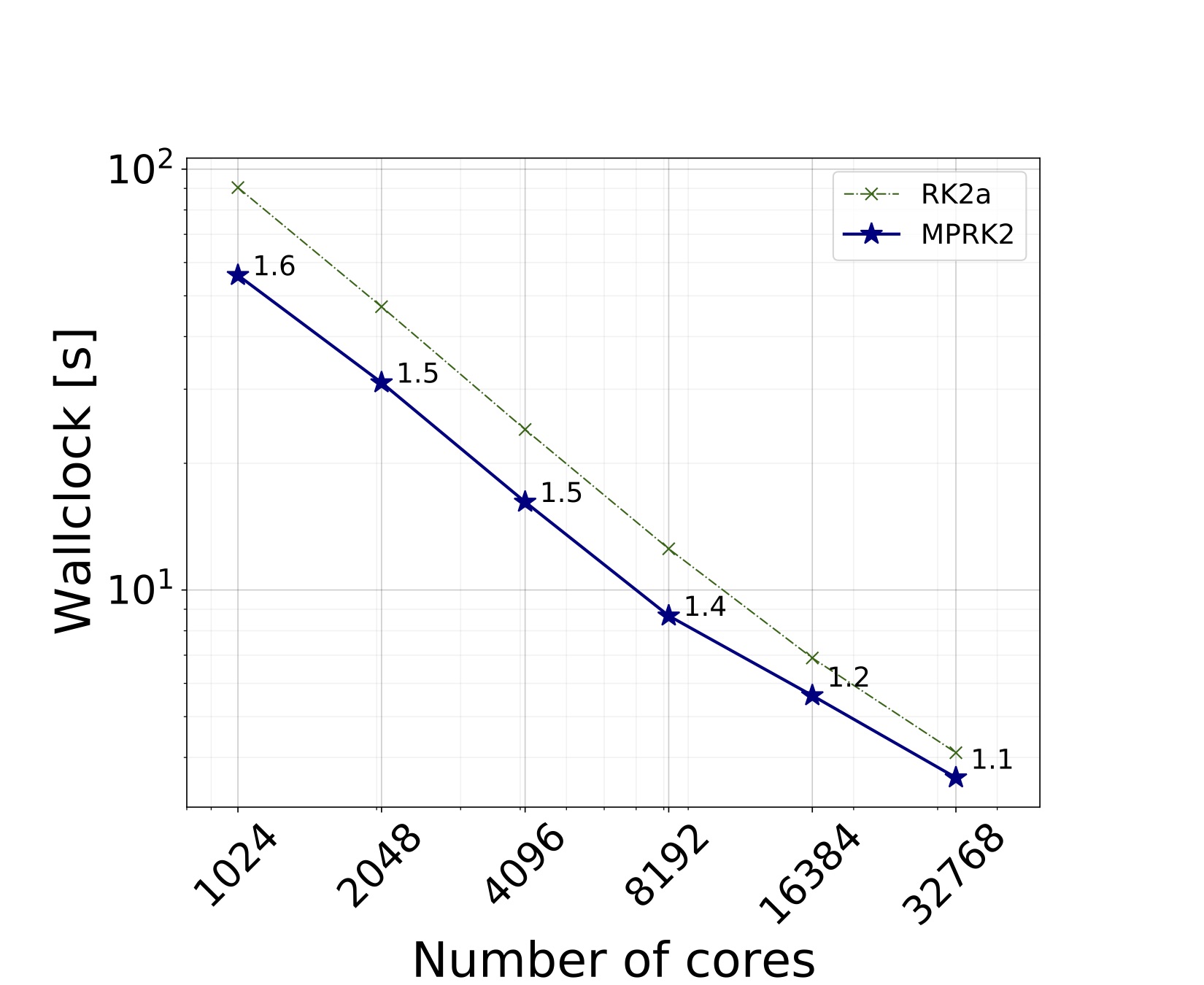
We also studied the parallel performance of the MPRK2 method using three-dimensional coupled compressible Navier-Stokes equations. Thanks to its explicit nature, the MPRK2 coupling method shows favorable strong and weak scaling results

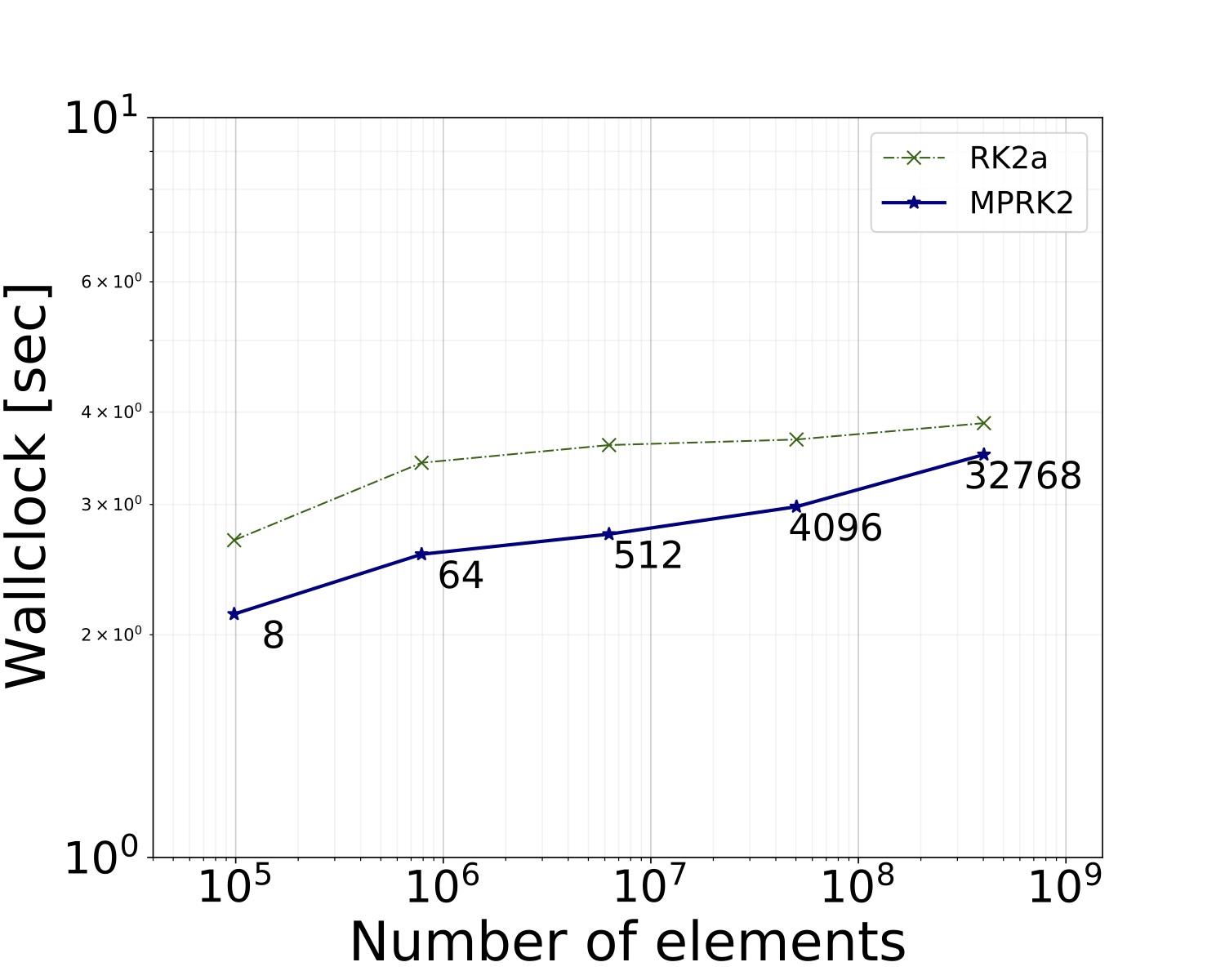
for the thermal convection example.

Entropy Stable IMEX and Multirate Methods

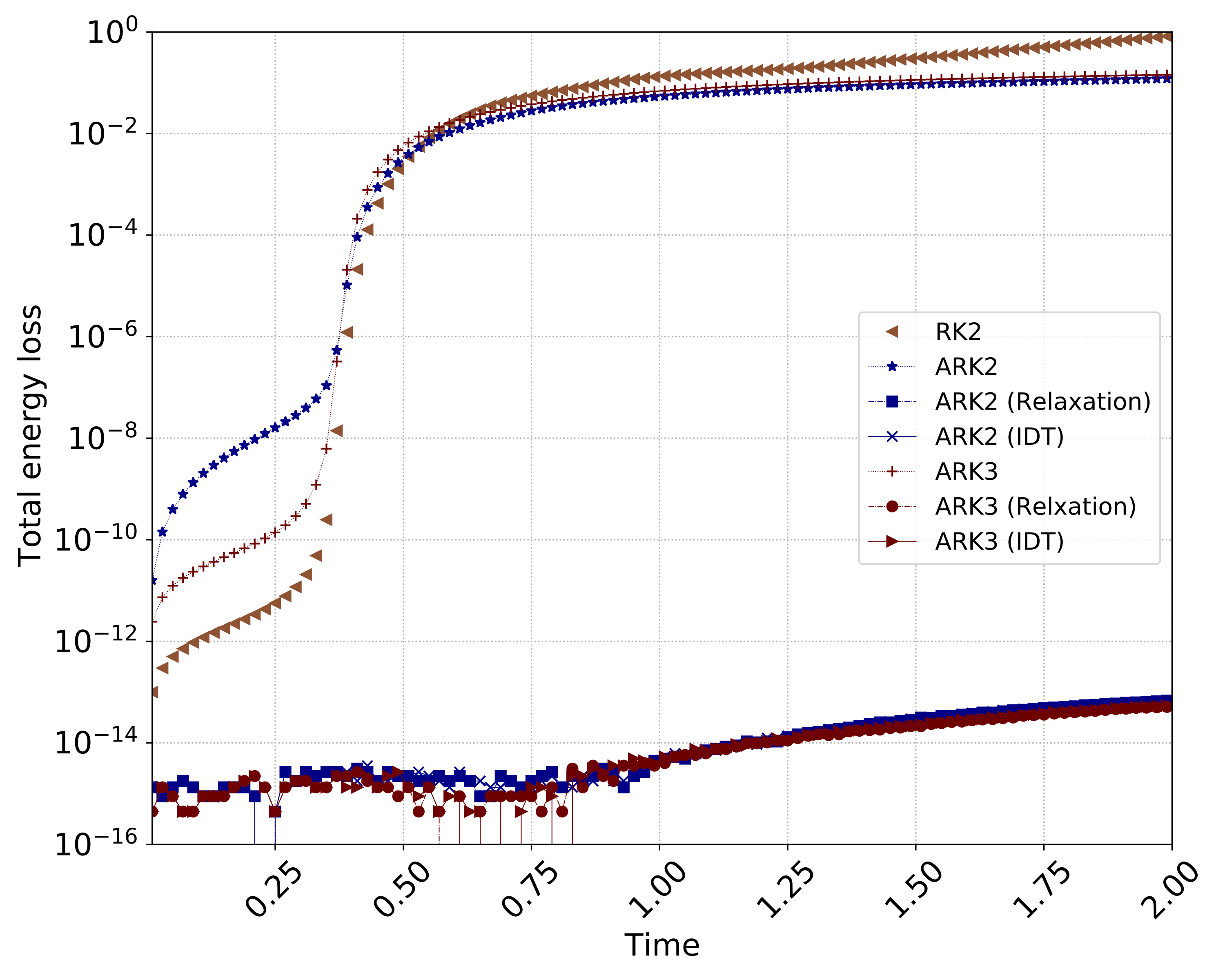
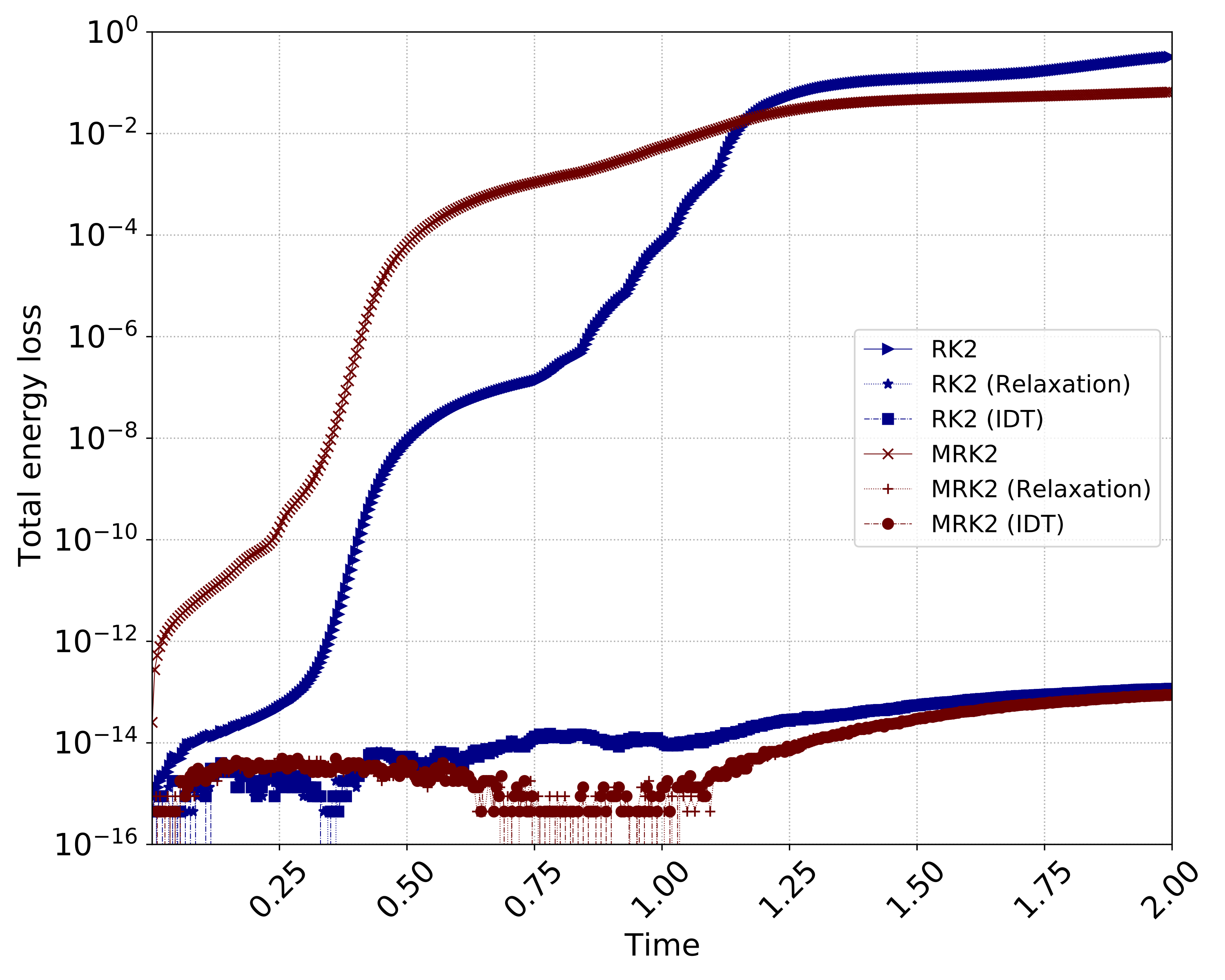
we present entropy-stable time discretization methods by using a relaxation method for partitioned Runge-Kutta schemes. In particular we apply relaxation to IMEX-RK methods to solve stiff problems and to a class of explicit second-order multirate methods with grid-induced stiffness. The relaxation methods successfully extend to both the IMEX-RK and multirate methods for targeting stiff problems in combination with an entropy-conserving/stable spatial discretization.

In particular, we focus on relaxation IMEX-RK methods on a uniform mesh to tackle scaleseparable stiffness. This is achieved by defining the linearized flux containing the fast wave in the system with the stiffness being implicitly treated, thus allowing for a longer time step size than that restricted by explicit methods. In addition, relaxation IMEX-RK methods not only support high-order accuracy in time but also have entropy-conserving/stable properties if entropy-conserving/stable fluxes are equipped with them.

We have also studied the multirate method on a nonuniform mesh to handle geometric-induced stiffness arising from mesh refinements. Unlike IMEX-RK methods, multirate methods do not require any linear/nonlinear solve and, hence, are attractive for parallel computing if proper preconditioning is not available. Multirate methods decompose the original problem into subproblems, where different time step sizes can be used locally on each subproblem. We have numerically demonstrated that the Relaxation-MRK2 method has a second-order rate of convergence and shows the total entropy-conserving/stable behavior if entropy-conserving/stable spatial discretization is provided.

Mass Conserving IMEX Coupling

Earth system models are composed of coupled components that separately model systems such as the global atmosphere, ocean, and land surface. While these components are well developed, coupling them in a single system can be a significant challenge. Computational efficiency, accuracy, and stability are principal concerns. In this study we focus on these issues. In particular, implicit-explicit (IMEX) tight and loose coupling strategies are explored for handling different time scales. For a simplified model for the air-sea interaction problem, we consider coupled compressible Navier–Stokes equations with an interface condition. Under the rigid-lid assumption, horizontal momentum and heat flux are exchanged through the interface.

IMEX coupling methods solve one domain explicitly and the other implicitly. To enhance computation efficiency, we adapt IMEX time integrators, which can handle scale-separable stiffness or geometrically induced stiffness, as an implicit solver. Furthermore, we employ a horizontally explicit and vertically implicit (HEVI) approach where solutions are obtained column by column; hence, the resulting linear system is significantly reduced compared with two-dimensional IMEX methods.

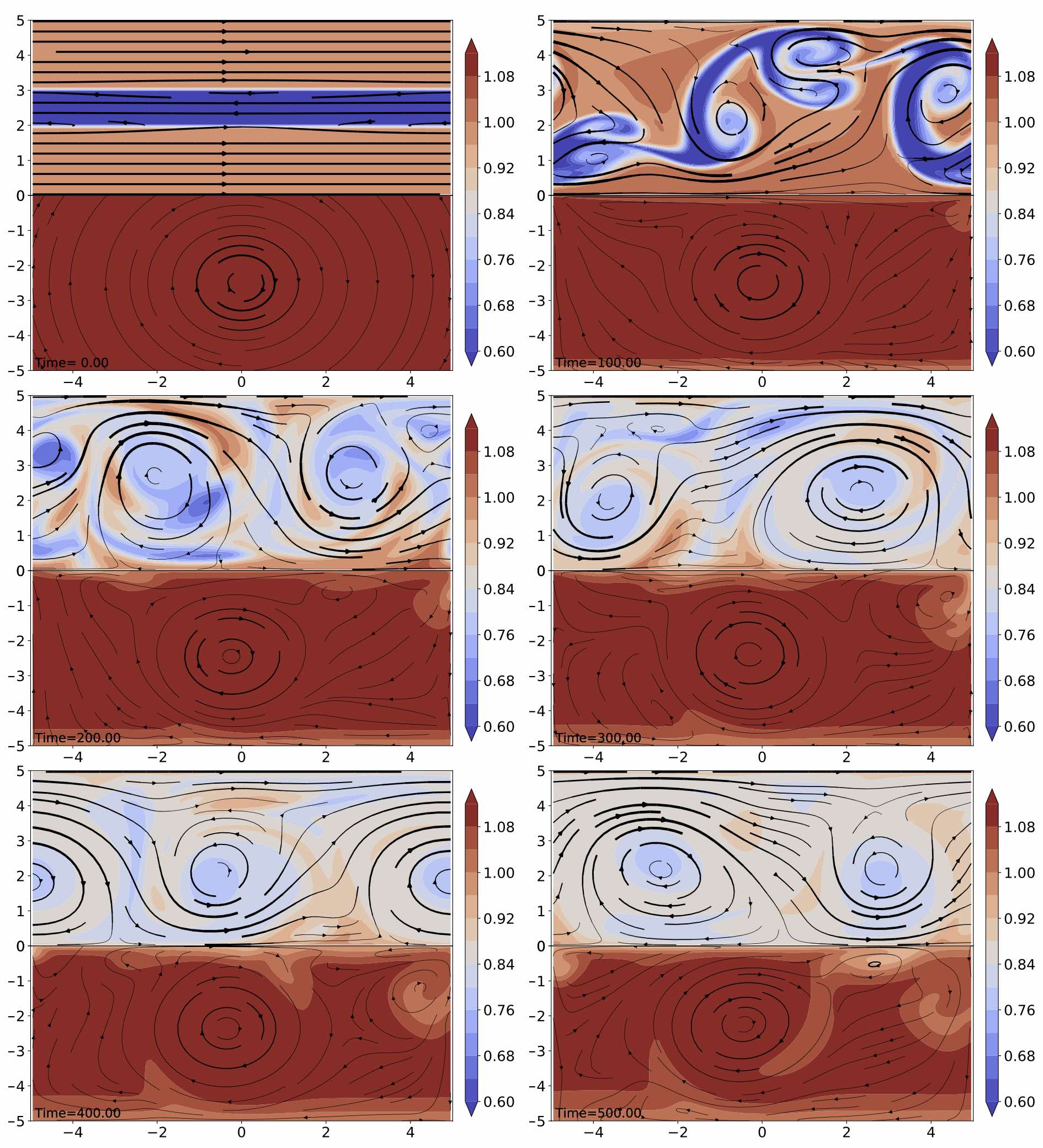
We conduct the simulation with the IMEX method. The evolution of temperature fields is shown for $t \in [0,500]$. Kelvin-Helmholtz waves are well developed at $t=100$ and start to diffuse while mixing fluids. Meanwhile, because of the heat and horizontal momentum exchange, fluid on the bottom domain cools near the interface and moves along the outside of vortex as time passes.

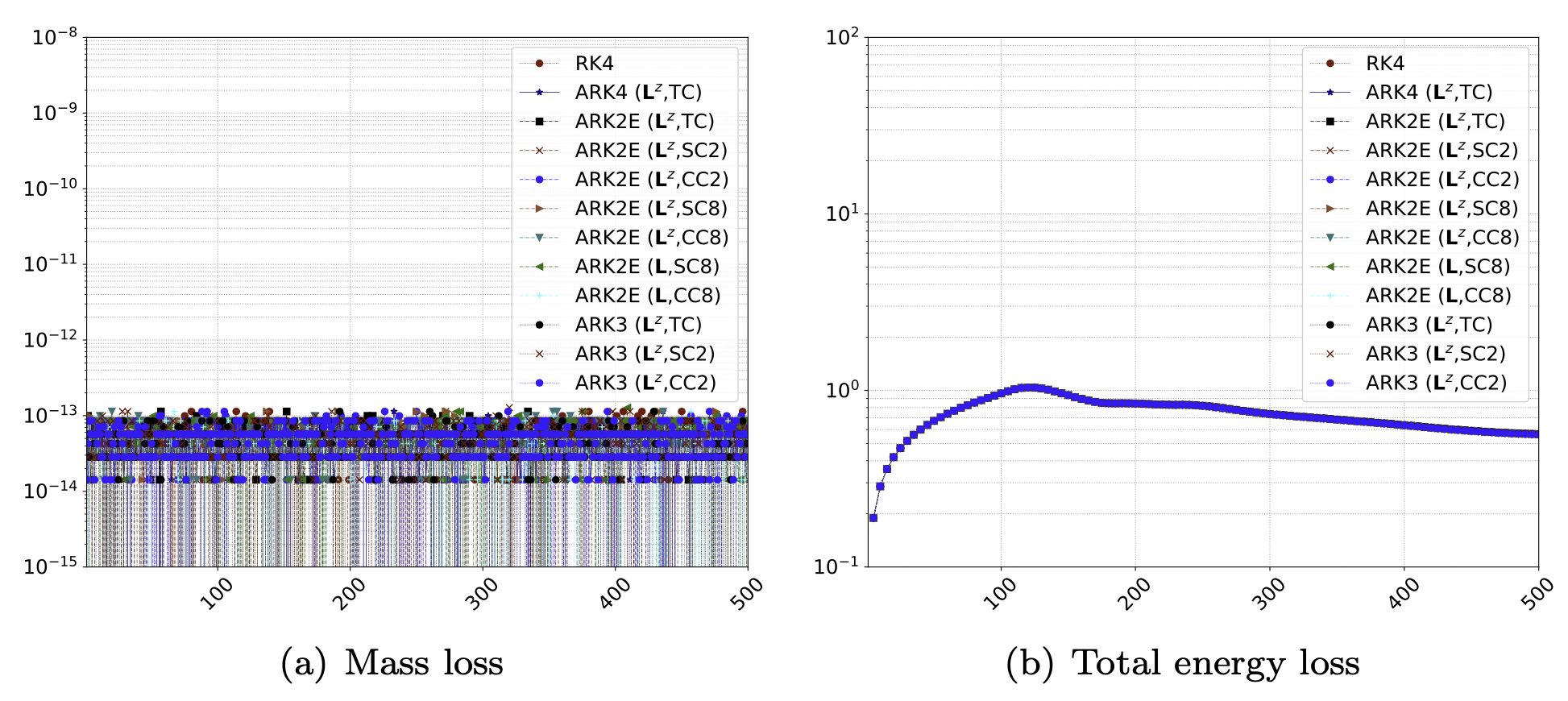
Total mass is conserved with IMEX coupling methods regardless of tight or loose coupling methods. The total mass losses for IMEX tight and loose coupling methods are within $\mathcal{O}(10^{−13})$. This result makes sense because we do not exchange the mass across the interface but adjust the wall temperature in the interface. This rigid-lid condition blocks the vertical motion of the interface: no mass flux is allowed, and hence the total mass is conserved. As for the total energy loss, a peak is observed near $t=100$ (when strong KHI is observed above), and then the total energy loss decreases as time passes.

Exponential DG

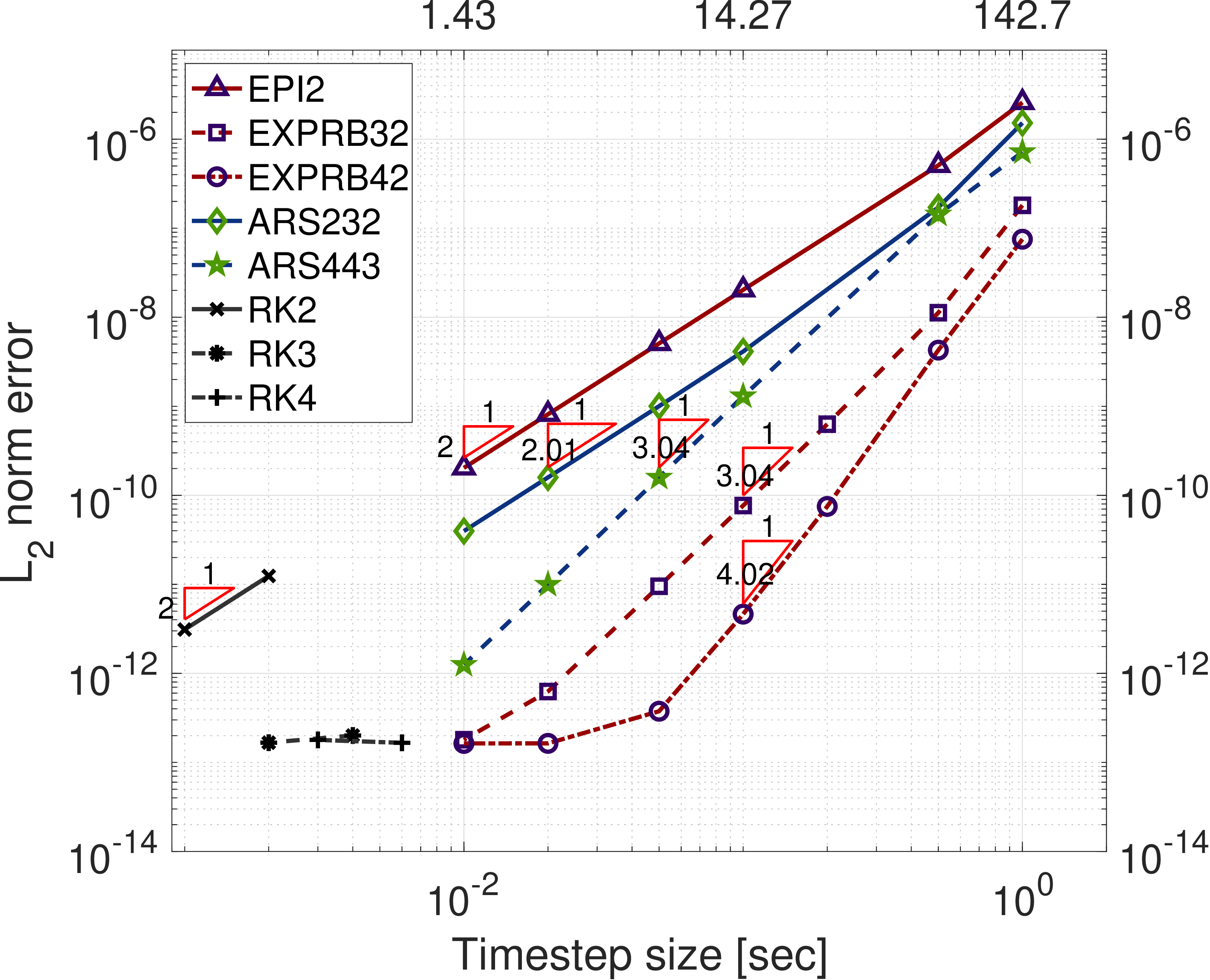
We propose an Exponential DG approach for numerically solving partial differential equations (PDEs). The idea is to decompose the governing PDE operators into linear (fast dynamics extracted by linearization) and nonlinear (the remaining after removing the former) parts, on which we apply the discontinuous Galerkin (DG) spatial discretization. The resulting semi-discrete system is then integrated using exponential time-integrators: exact for the former and approximate for the latter.

By construction, our approach is stable with a large Courant number (Cr > 1); supports high-order solutions both in time and space; is computationally favorable compared to IMEX DG methods with no preconditioner; and requires comparable computational time compared to explicit RKDG methods.

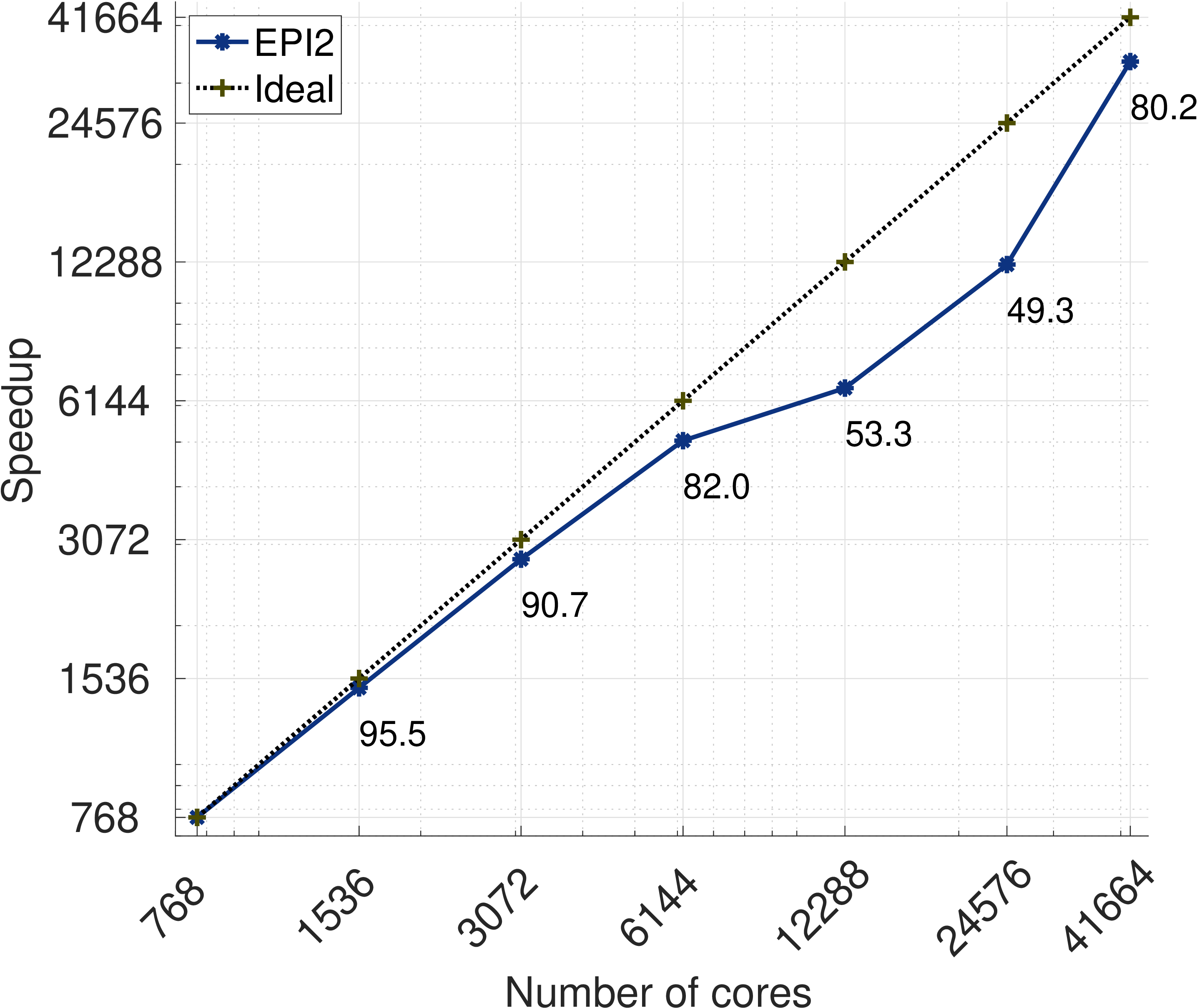
Exponential DG approach is scalable in a modern massively parallel computing architecture by exploiting Krylov-subspace matrix-free exponential time integrators and compact communication stencil of DG methods. The following plot shows good strong scalability up to 41664 cores (the maximum number of cores in Skylake system in TACC). An isentropic vortex is simulated for three-dimensional Euler equations.

Hybridized DG methods for a Linear Degenerate Elliptic Equations

We develop a high-order hybridized discontinuous Galerkin (HDG) method for a linear degenerate elliptic equation arising from a two-phase mixture of mantle convection or glacier dynamics. Both phenomena can be described by a two-phase mixture model, in which the mixture of the fluid and the solid is described by the porosity $\phi$(i.e., $\phi>0$ implies the fluid-solid two-phase and $\phi=0$ means the solid single-phase region). The challenge is when the porosity vanishes because the system degenerates, which make the problem difficult to solve numerically. We start by scaling variables to obtain the well-posedness. Then we spatially discretize the system using the upwind HDG framework.

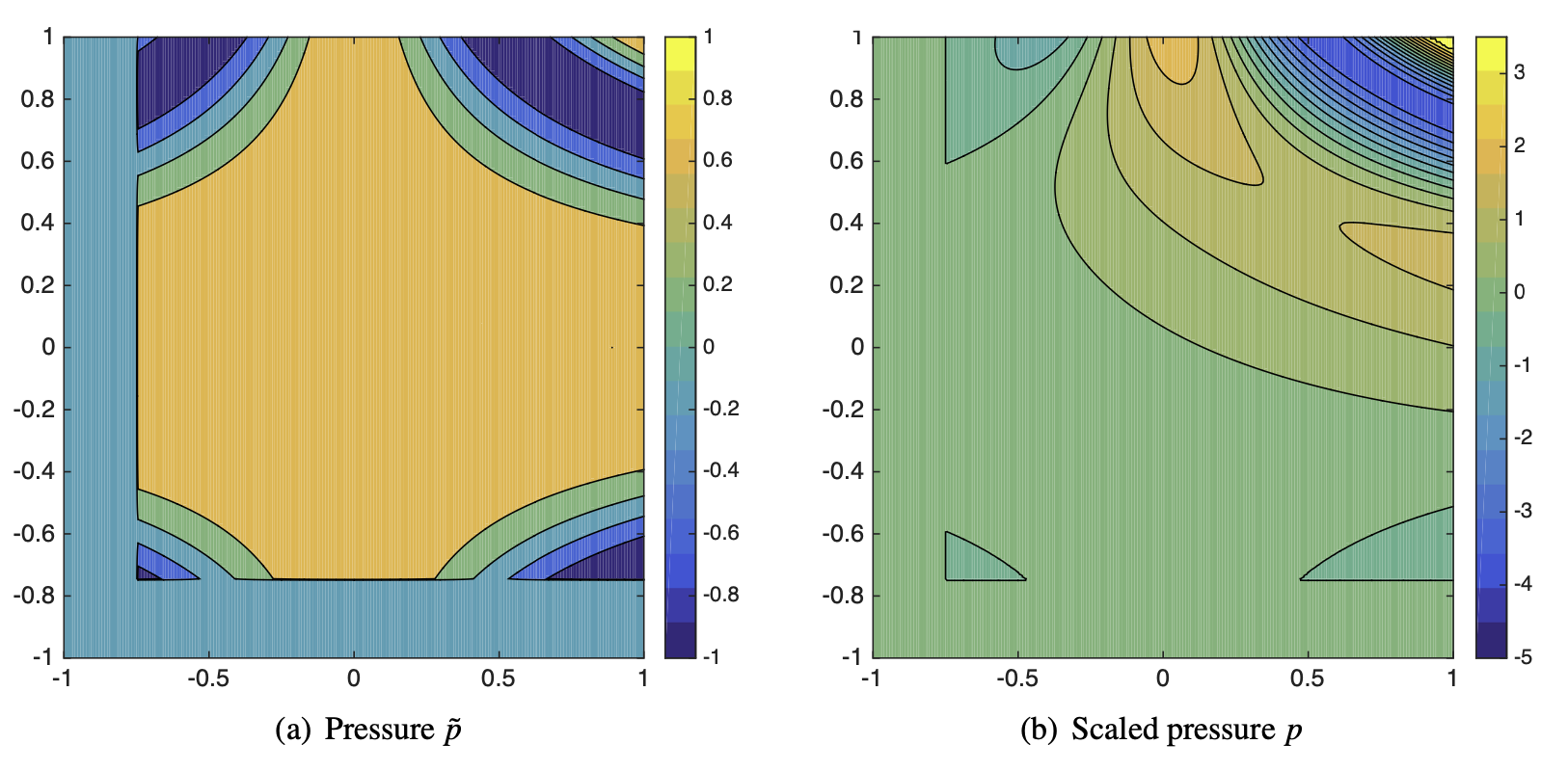
Below shows the contours of the physical pressure $\tilde{p}$ and the scaled pressure $p$. We observe that the pressure $\tilde{p}$ changes smoothly in the two-phase regions, but abruptly becomes zero in the one-phase region. The sudden pressure jump on the intersection is alleviated with the use of the scaled pressure $p$.

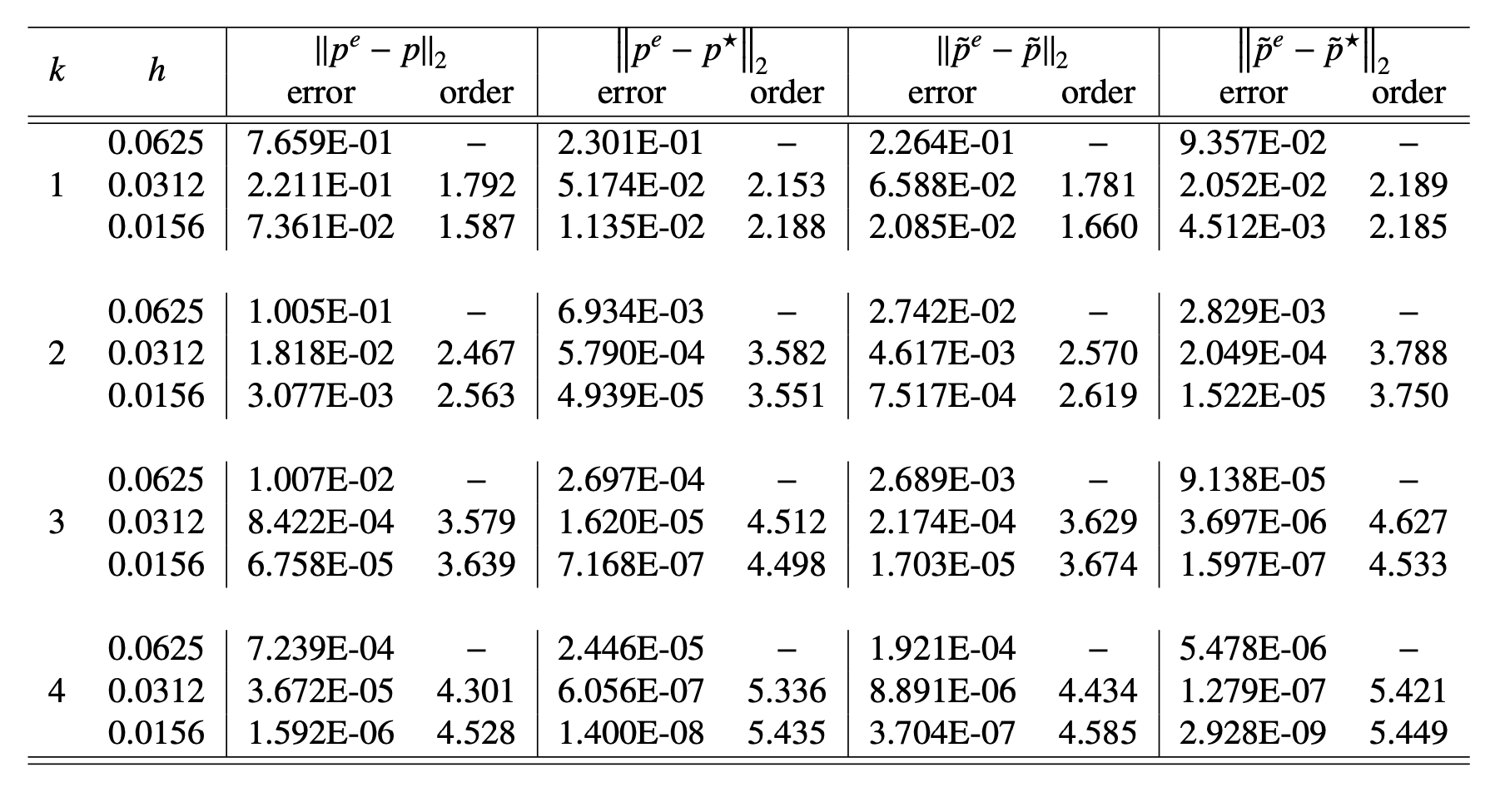
We have modified the upwind HDG flux to accommodate the degenerate (one-phase) region. When the porosity vanishes, the unmodified HDG system becomes ill-posed because the stabilization parameter associated with the HDG flux disappears. To handle this, we introduce the generalized stabilization parameter that is composed of the upwind based parameter in the two-phase region and a positive parameter in the one-phase region. This enabled us to develop a high-order HDG method for a linear degenerate elliptic equation. For the degenerate case with a smooth solution, the convergence rate of $k + \frac{1}{2}$ is observed for the scaled pressure $p$. We can further enhance the HDG solutions in smooth-regions by post-processing. The post-processed pressure $p^\star$ converges to the true solution with the rate of $k + \frac{3}{2}$.

A Coupled Implicit HDG and Explicit DG methods for Shallow Water Systems

We propose IMEX HDG-DG schemes for planar and spherical shallow water systems. Of interest is subcritical flow, where the speed of the gravity wave is faster than that of nonlinear advection. In order to simulate these flows efficiently, we split the governing system into a stiff part describing the gravity wave and a non-stiff part associated with nonlinear advection.

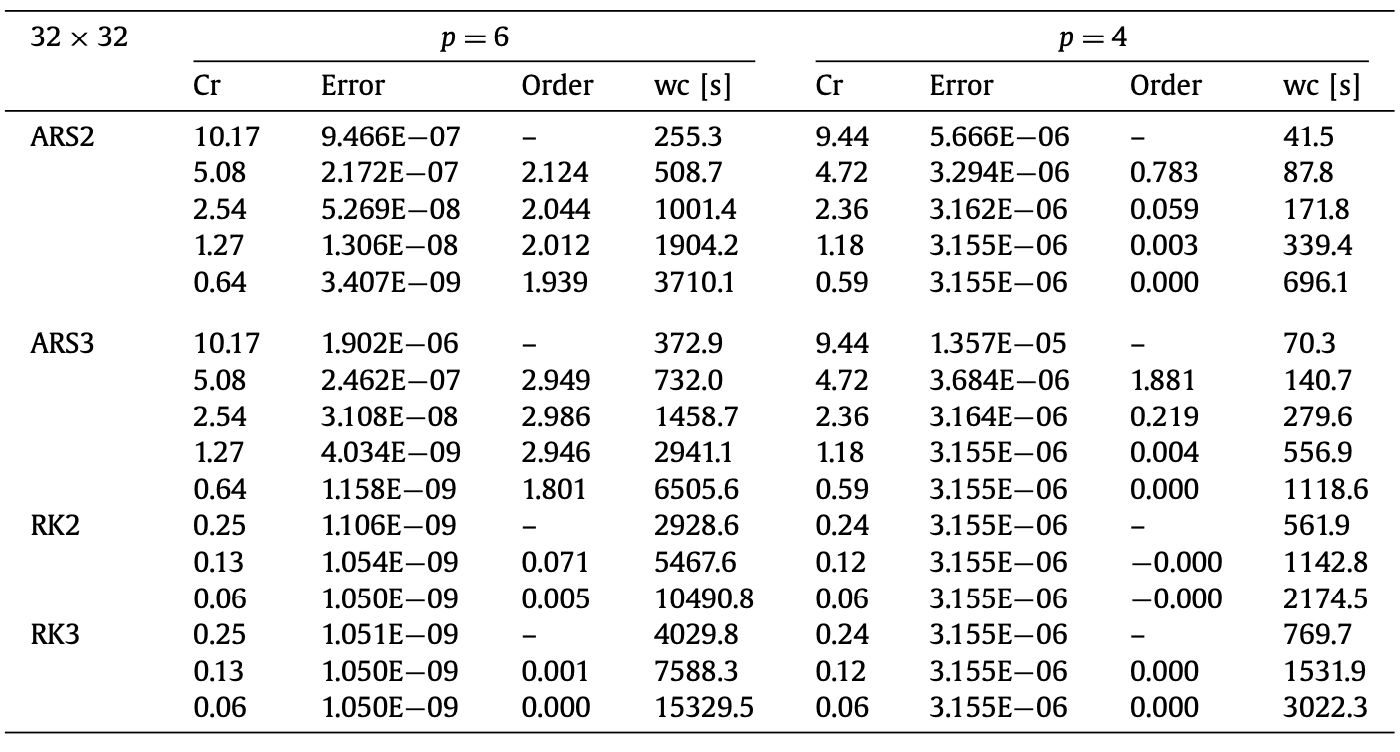
IMEX HDG-DG approaches are more economical than our previous work on IMEX DG due to the fewer number of coupled degrees of freedom in the context of a direct solver. Compared to standard fully implicit methods, they are advantageous since only one linear solve is needed for each stage per time-step. With a low Froude number, the IMEX HDG-DG methods can be more economical than the explicit RK when the desired accuracy is relaxed. Below is the summary of temporal convergence study for moving vortex with $Fr=0.01$. When the saturation error level is $\mathcal{O}(10^{-6})$, ARS2 and ARS3 are six and four times faster than RK2 DG.

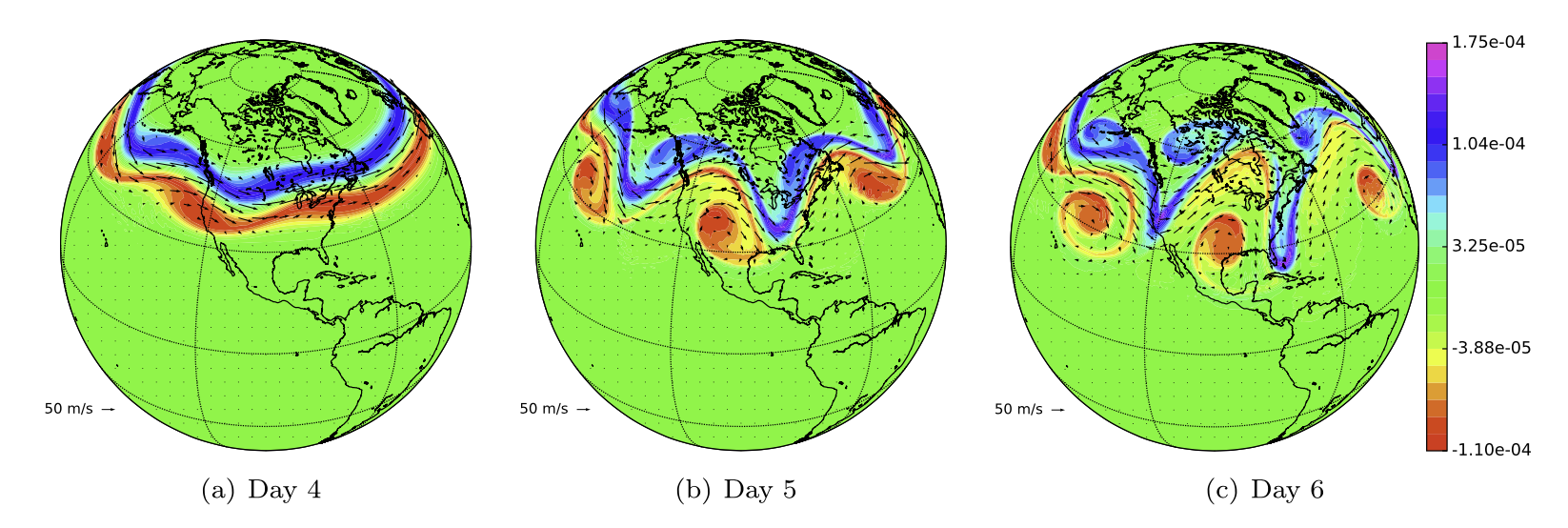
A zonal jet, a wind field along a latitude line and geostrophically balanced height field, is initialized in the northern hemisphere. Then, the height field is perturbed by adding a smoothly localized bump to the center of the jet, which causes barotropic waves to evolve in time. The vorticity field computed from ARS2 HDG-DG is comparable to the work.

Temperature and Moisture Retrievals from Hyperspectral Measurements

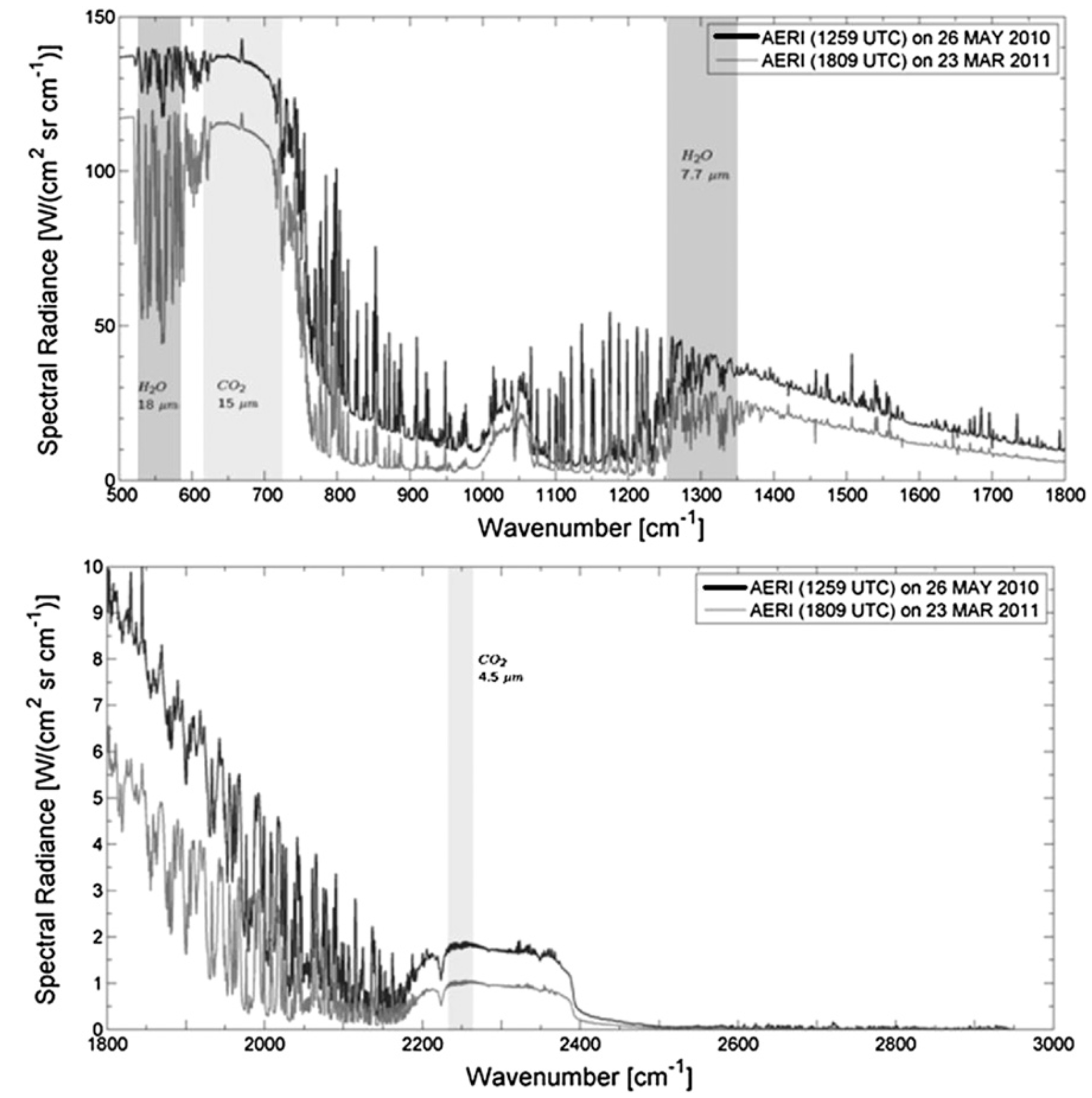
An Atmospheric Emitted Radiance Interferometer (AERI), which measures downwelling radiances, has been in operation at Anmyeon-do, South Korea, since June 2010. Temperature and moisture profiles with high temporal and vertical resolution can be retrieved from the measured AERI spectrum through the retrieval algorithm AERIPROF.

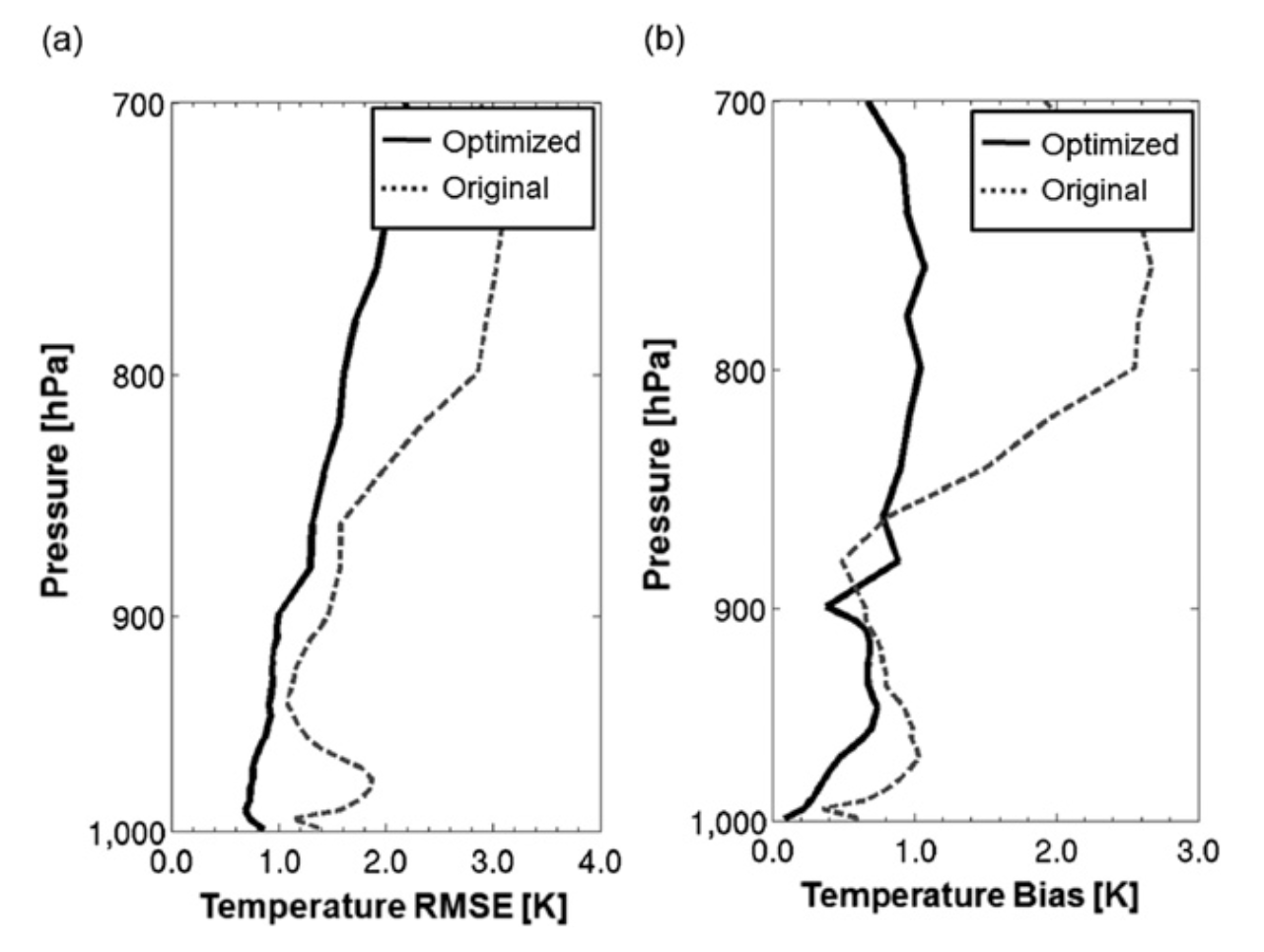
Below shows the spectra measured by the AERI on 26 May 2010 (case 1) and on 23 March 2011 (case 2). The air temperature at ground level in case 1 ($290.8 K$) was larger than in case 2 ($276.7 K$). Precipitable water vapor (PWV) in case 1 ($2.02 cm$) was higher than in case 2 ($0.38 cm$). The $CO_2$ bands are sensitive to a temperature sounding. The radiances in the $CO_2$ bands are higher in case 1 than in case 2. The transparency of the $H_2O$ bands and the atmospheric window is sensitive to the column water amount. The transparency of the $H_2O$ bands and the atmospheric window bands in case 1 is reduced compared to case 2 counterpart. The two measured spectra show good agreement with the observed temperature and PWV.

In this work, we improve retrieval performance by adjusting a bias spectrum and regression coefficients for Anmyeon-do. The bias spectrum was recomputed from the coincident radiosondes during the field experiments and regression coefficients were obtained from local radiosondes and associated simulated spectral radiances through principal component analysis (PCA). The reduced (a) RMS errors and (b) bias profiles between the radiosondes are observed. The modified statistical regressions show better performance than the original statistical regression in the lower troposphere ($1000–700 hPa$).